Сюда переношу все, что связано со статистикой и нужно было на практике – в тестировании, разработке и в других инженерных задачах.
Арифметической прогрессией (арифметической последовательностью) – последовательность с фиксированным инкрементом. Для меня
Арифметической прогрессией (арифметической последовательностью) - называется последовательность чисел a1,a2,...,an, каждое из которых, начиная с a2, получается из предыдущего прибавлением к нему одного и того же постоянного числа d (разность прогрессии), то есть:An=An−1+D. - Если известен первый член прогрессии и её разность, то n-ый член арифметической прогрессии находится по формуле An=A1+D(n−1). - Сумма первых (т.е. только для последовательности integer с шагом 1) элементов находится по формуле n*(n+1)/2. Для меня наиболее интуитивно проще запоминаема "формула юного Гауса" - складываем последнее число и первое, умножаем на половину элементов. Действительно, числа от 1 до 100, можно разбить на 50 пар, сумма в которых равна 101: 1+100=101,2+99=101,3+98=101,…50+51=101. # example 100, 110, 120, 130, 140, 150, 160, 170, 180 # calc n-member a_9 = 100 + 10 * (9-1) = 180 # example2 1, 2, 3, 4, 5, 6, 7, 8, 9 # calc sum of members a_sum = (9 * 10)/2 = 45
Двоичным (булевым) n-мерным вектором – двоичная последовательность.
Двоичным (булевым) n-мерным вектором называют набор из n чисел (b1, b2, ..., bn), каждое из которых может принимать только значения в двоичной системе счисления – 0 или 1. Двоичный вектор является обратным (инвертированным), если он образован из заменой всех нулей единицами, а единиц – нулями. Например, если вектор равен (0,1,1,1,0,1), то инвертированный (1,0,0,0,1,0).
В позиционных системах счисления значение цифры зависит от ее положения — позиции — в числе. Например, число 15 обозначает пятнадцать, 51— пятьдесят один. Первая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричная, т.е. в ней использовалось шестьдесят цифр. Мы до сих пор считаем, час – 60 минут, минута – 60 секунд, окружность – 360∘. Позиционные системы счисления позволяют легко производить арифметические расчеты. Представление чисел с помощью арабских цифр — самая распространенная позиционная система счисления, она называется десятичной системой счисления потому, что использует десять цифр: 0,1,2,3,4,5,6,7,8 и 9. Количество цифр, используемое в системе счисления, называется ее основанием. В десятичной системе основание равно десяти, в двоичной системе — двум, ну а в восьмеричной и шестнадцатеричной — соответственно, восьми и шестнадцати
Перевод в десятичную Перевести двоичное число 111111 в десятичную систему счисления. 2^5 + 2^4 + 2^3 + 2^ 2 + 2^1 + 2^0 = 127
Перевести число из шестнадцатеричной системы счисления 1AF2 в десятичную систему счисления.
(1 * 16^ 3) + (10 * 16 ^ 2) + (15 * 16 ^ 1) + (2 * 16^ 0) = 6898
Перевод из десятичной
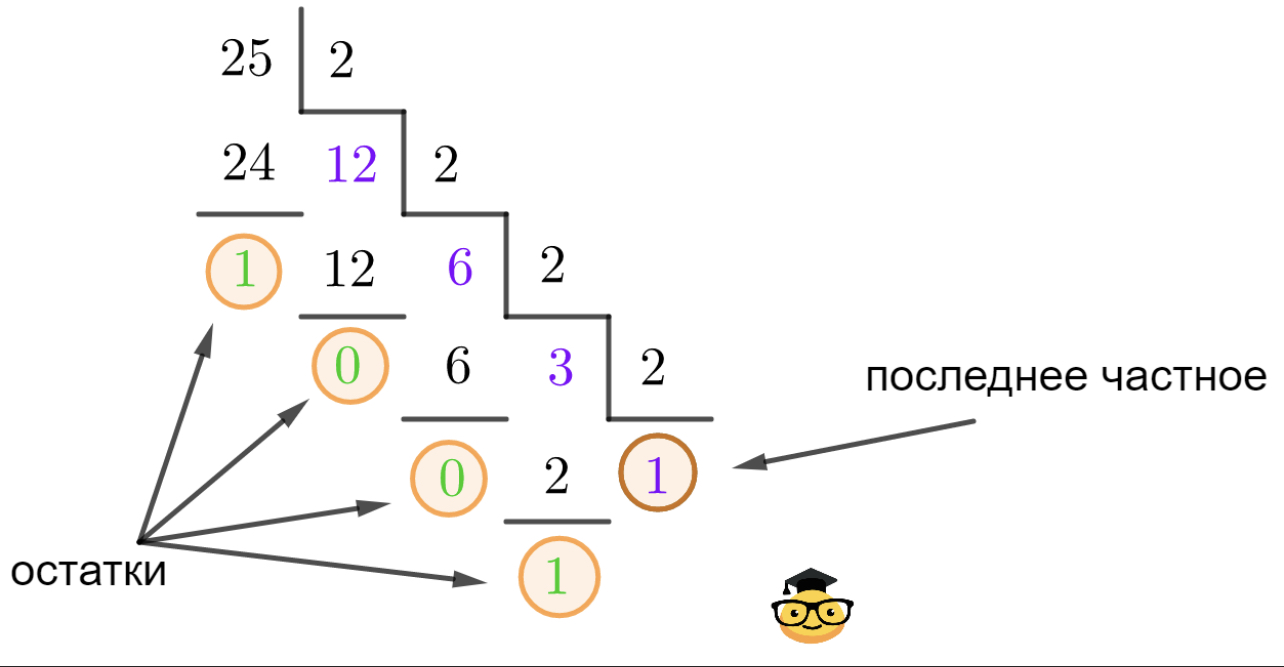
Перевести десятичное число 25 в двоичную систему счисления.
11001
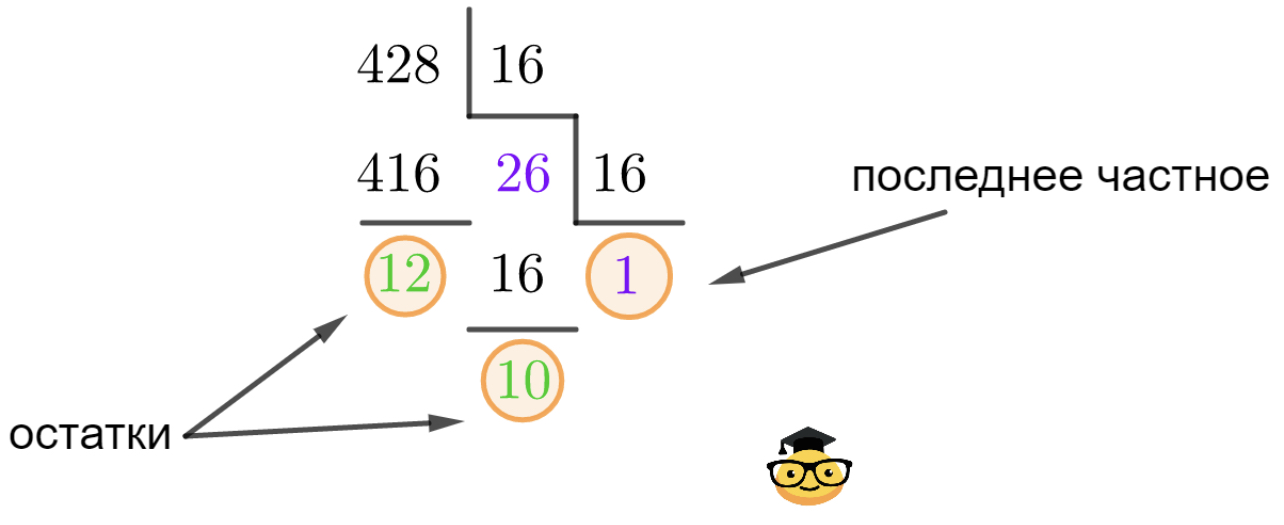
Перевести десятичное число 428 в шестнадцатеричную систему счисления.
1AC
В непозиционных системах счисления значение цифры не зависит от ее положения — позиции — в записанном числе. Примером непозиционной системы счисления является римская система (см. примечание). При использовании непозиционных систем счисления очень сложно выполнять математические расчеты и необходимо большое количество различных знаков для записи чисел, особенно больших.
Для записи чисел в римской системе используются два правила:
- каждый меньший знак, поставленный слева от большего, вычитается из него;
- каждый меньший знак, поставленный справа от большего, прибавляется к нему.
число 444 в римской системе счисления будет записано в виде CDXLIV=(500−100)+(50−10)+(5−1)=400+40+4(три группы второго вида).
Денежные знаки — пример смешанной системы счисления. Сейчас в России используются монеты и купюры следующих номиналов: по 1, 2, 5, 10, 50, 100, 200, 500, 1000, 2000, 5000 рублей и по 5,10,50 копеек. Чтобы получить некоторую сумму в рублях, нужно использовать некоторое количество денежных знаков различного достоинства. Таким образом, у этой системы целый ряд оснований, равный достоинствам денежных знаков, также используется основание той системы, с помощью которой производится их счет.
Геометрической прогрессией – последовательность с фиксированным множетелем.
Геометрической прогрессией - это последовательность, первый член которой не равен нулю, а каждый последующий член равен произведению предыдущего члена на некоторое фиксированное ненулевое число (называемое знаменателем геометрической прогрессии q). Любой член геометрической прогрессии может быть вычислен по формуле Bn = B1*q^(n-1) # example 3, 12, 48, 192, 768, 3072 # calc n-member a_6 = 3 * 4^5 = 3072
Коэффициент корреляции (correlation coefficient) – Корреля́ция (от лат. correlatio «соотношение»), или корреляцио́нная зави́симость — статистическая взаимосвязь двух или более случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин ((почему это важно – в wiki)). Пример расчета в python.
| Количественная мера тесноты связи |
Качественная характеристика силы связи |
| 0,1-0,3 | Слабая |
| 0,3-0,5 | Умеренная |
| 0,5-0,7 | Заметная |
| 0,7-0,9 | Высокая |
| 0,9-0,99 | Весьма высокая |
Размах (range) – арифметическая разница между максимальным и минимальным значением выборки, максимальное расстояние между значениями ряда/выборки. Причем по моей практике чаще полезно не просто абсолютное значение размаха, а процент размаха от минимального до максимального (размах_в_% = (макс-мин)/мин * 100) – он показывает на сколько минимальная величина отклоняется от максимального в процентах или другими словами мы знаем сколько добавить к минимуму процентов от минимума, чтобы получить максимум (макс = мин + мин * размах_в_%). Размах в процентах одинаково нагляден как при небольшом размахе, так и при весомом, в отличии от “во сколько или на сколько раз”.
https://en.wikipedia.org/wiki/Range_(statistics) In statistics, the range of a set of data is the difference between the largest and smallest values. Sample RANGE : The spread (distance or value) from the lowest to the highest value in the sample.
Если требуется перевести число из десятеричной системы в двоичную, необходимо сделать следующее:
1) Последовательно делить это число на два, каждый раз записывая результат в виде целого числа и остатка.
2) Деление продолжать до тех пор, пока в результате не останется единица.
Итоговое число получается путём последовательной записи результата последнего деления и остатков всех делений в обратном порядке. Пример кода см. тут.
Сложением отрицательных чисел в любом случае всегда будет являтся отрицательное число: -1 + -1 = -2
Средние величины

Среднее арифметическое числе A, B:
(A + B)/N
Среднее квадратичное числе A, B:
sqr((A^2 + B^2)/N)
Среднеквадратическое отклонение (СКО) – наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания ((среднего значения)). Обычно он означает квадратный корень из дисперсии случайной величины, но иногда могут означать тот или иной вариант оценки этого значения.
Нужно уметь применять статистику (с этим часто проблема) и если задача найти максимальное расстояние между значениями ряда/выборки – то среднеквадратичное отклонение не подходит, нужно считать размах (выше про него).
Встречаются также синонимы словосочетания среднеквадрати́ческое отклоне́ние, как то́: среднее квадрати́ческое отклоне́ние; среднеквадрати́чное отклоне́ние; квадрати́чное отклоне́ние; станда́ртное отклоне́ние; станда́ртный разбро́с.
Очень хорошо описано в wiki, включая то, что не добавил сюда – пример расчета величины среднеквадратичного отклонения (расчет среднего, расчет квадрата отклонений каждой величины, расчет дисперсии в виде среднего от квадратов отклонений, расчет отклонения в виде корня дисперсии), примеры из жизни, когда оно может использоваться (погода, спорт, экономика).
Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, а дисперсия измеряется в квадратах этой единицы измерения. Большее значение среднеквадратического отклонения показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.
Например, у нас есть три числовых множества: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8}. У всех трёх множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.
# Excel
=СТАНДОТКЛОН.Г(0;0;14;14) # 7
=СТАНДОТКЛОН.Г(0;6;8;14) # 5
=СТАНДОТКЛОН.Г(6;6;8;8) # 1
В общем смысле среднеквадратическое отклонение можно считать мерой неопределённости. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.
Натуральные числа – числа, которые могут быть получены в результате счета предметов (целочисленные неотрицательные от одного). Натуральные числа можно разделить на три класса (как простых, так и составных чисел бесконечно много):
-
- единица (имеет один натуральный делитель),
- простое число (имеет два натуральных делителя) – число является простым, если оно не имеет делителей, кроме 1 и самого себя.
- составное число (имеет более двух натуральных делителей)[1].
Цифровой корень числа n получается следующим образом: если сложить все цифры этого числа, затем все цифры найденной суммы и повторять этот процесс до тех пор, пока в результате не будет получено однозначное число (цифра), которое и называется цифровым корнем изначального числа. Используется в нумералогии.
Извлечение корня – операция, обратная возведению в степень. По умолчанию в python вычисляется квадратный корень – какое число (9) нужно возвести во ^2 степень, чтобы получить передаваемое (81).
>>> math.sqrt(4) 2.0 >>> math.sqrt(81) 9.0 >>> math.sqrt(100) 10.0
Процент одного числа от другого – часто есть задача сколько составляет число X от числа Y. Формула расчета простейшая, но зачастую (float, большие значения int) быстрее скопипастить. Удобный калькулятор.
Формула: (x/y) * 100
Человеческого вида (human readable) процент как число при программировании – полученный в human readable форме процент с точки зрения кода проще всего представлять как 25/77/99% = 25/100, 77/100, 99/100. Если же логика процента встроена в код/хранится в базе в нормальном виде – то более логично использовать уже сам результат этого деления 25/77/99% = 0.25/0.77/0.99.
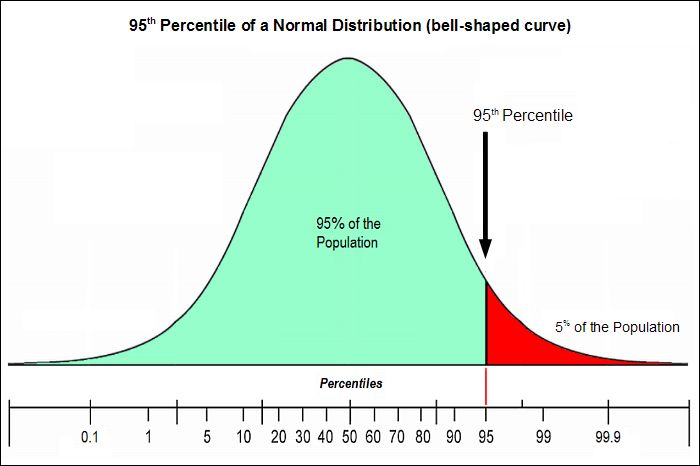
Перцентиль, процентиль (percentile) – это сотая доля объема измеренной совокупности, выраженная в процентах. Процентиль позволяет понять как данные распределены разделив их на 100 долей. Частные случаи:
-
- Медиана – это 50ый процентиль.
- Cамое большое значение в исходном наборе данных – 100-й процентиль.
- Самое малое значение – 0-й.
Например, пятый процентиль охватывает 5% объема выборки. Предположим, показатель Ивана равен пятому процентилю. Это означает, что Иван написал тест лучше, чем 5% студентов. Процентиль (или центиль ) - это показатель, используемый в статистике , указывающий значение, ниже которого падает данный процент наблюдений в группе наблюдений. Например, - 20-й процентиль - это значение (или балл), ниже которого могут быть обнаружены 20% наблюдений. Эквивалентно 80% наблюдений находятся выше 20-го процентиля. - 80-й процентиль - 20% наблюдений находятся выше 80-го процентиля.
Используется в нагрузочном тестировании (напр. JMeter) как метрика, не скрывающая всплески/выбросы (outliers), в отличии от среднего значения.
Пример расчета перцентиля/процентиля
-
- Логика расчета и три разных способа расчета (могут давать разный результат!) хорошо описаны тут
- Расчет самый простой в Excel, автоматизация расчета возможна с использованием python + numpy, python + pandas. Пример расчета перцентиля 80,90,95,99 поведение в случае выборки с “выбросом”.
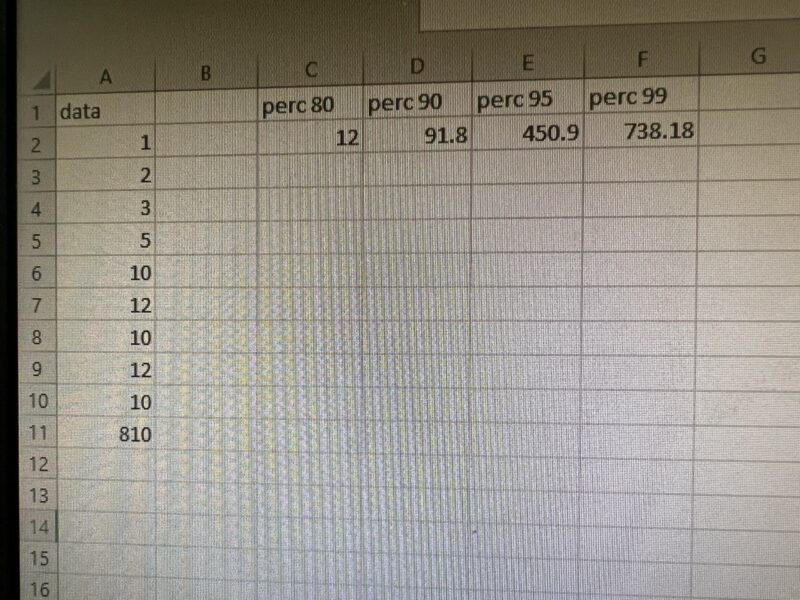
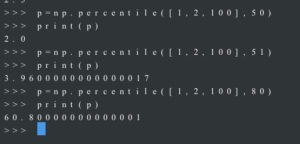
- Сложнее посчитать самому, но вполне возможно
Пример расчета значения 50-го процентиля (медианы) для набора 1, 2, 3, 4, 5 разными способами.
# EXCEL
=PERCENTILE.INC({1;2;3;4;5};0,5) = 3
=PERCENTILE.EXC({1;2;3;4;5};0,5) = 3
=ПРОЦЕНТИЛЬ.ВКЛ({1;2;3;4;5};0,5) = 3
=ПРОЦЕНТИЛЬ.ВЫКЛ({1;2;3;4;5};0,5) = 3
# PYTHON
>>> import numpy as np
>>> a = np.array([1,2,3,4,5])
>>> p = np.percentile(a, 50)
>>> print(p)
3.0
# Ручной расчет - самый простой (не точный, но значения будут близки или равны получаемым в excel/python):
1) Сортируем массив данных по возрастанию и нумеруем (ранжируем, присваиваем номер) результат сортировки 2) Определяем номер/ранг на основе заданного процентиля n = ceil(P/100 * N) 2.1) P - искомый процентиль 2.2) N - общее количество номеров/рангов 3.3) n - ранг 3) Значение соответствующее рангу считаем процентилем
1 значение - 1 ранг
2 значение - 2 ранг
3 значение - 3 ранг
4 значение - 4 ранг
5 значение - 5 ранг
n = 50/100 * 5 = ceil(2.5) = 3
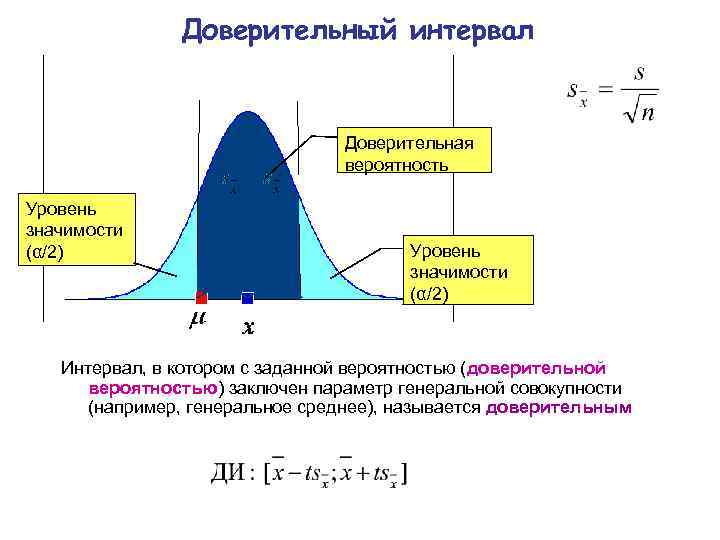
Доверительный интервал – интервал, в котором с заданной вероятностью (доверительной вероятностью) заключен параметр генеральной совокупности (напр. генеральное среднее). Доверительная вероятность выражается числом от 0 до 1 или в процентах, например 90%, 95%, 99% и показывает вероятность того, что действительное значение исследуемой переменной будет лежать в принятом (указанном) диапазоне.
Среднее значение (average/mean) – сумма значений элементов поделенная на два:
(N1 + N2 + N3)/2
Средневзвешанное значение (weighed average/mean) – когда элементы не равноценны т.к. если веса всех элементов равны – это простое среднее. Используется часто на практике – например, расчет NSS LABS throughput, расчет IMDB score. Пример расчет, когда вес первого 0.9, второго 1.2, третьего 2.2:
(N1*0.9 + N2*1.2 + N3*2.2)/2
NSS Labs The weighted arithmetic mean is similar to an ordinary arithmetic mean (the most common type of average), except that instead of each of the data points contributing equally to the final average, some data points contribute more than others. The notion of weighted mean plays a role in descriptive statistics and also occurs in a more general form in several other areas of mathematics. If all the weights are equal, then the weighted mean is the same as the arithmetic mean. IMDb Weighted Average Ratings IMDb publishes weighted vote averages rather than raw data averages. The simplest way to explain it is that although we accept and consider all votes received by users, not all votes have the same impact (or ‘weight’) on the final rating. When unusual voting activity is detected, an alternate weighting calculation may be applied in order to preserve the reliability of our system. To ensure that our rating mechanism remains effective, we do not disclose the exact method used to generate the rating.
Медиана — это значение признака, справа и слева от которого находится равное число наблюдений (по 50%, 50ый процентиль). Для получения значения, которое находится по середине выборки правильнее использовать медиану, а не среднее значение. Потому что среднее не учитывает выбросы (outliers), в отличии от медианы.
Рассчитать медиану для числового ряда просто (не говоря про python функции, с ними пример ниже): Например, медианой набора {11, 9, 3, 5, 5} является число 5, так как оно стоит в середине этого набора после его упорядочивания: {3, 5, 5, 9, 11}. Если в выборке чётное число элементов, медиана может быть не определена однозначно: тогда для числовых данных чаще всего используют полусумму двух соседних значений – то есть медиану набора {1, 3, 5, 7} принимают равной 4 (пример №2 расчета в Excel для такого случае ниже). Можно также сказать, что медиана является 50-м персентилем, 0,5-квантилем или вторым квартилем выборки или распределения.
Медиа́на (от лат.mediāna «середина») набора чисел — число, которое находится в середине этого набора, если его упорядочить по возрастанию, то есть такое число, что половина из элементов набора не меньше него, а другая половина не больше. Пример №1 (python) Среднее для ряда 1 2 6 = 3 Медиана для ряда 1 2 6 = 2 >>> import statistics >>> l = [1,2,6] >>> statistics.mean(l) 3 >>> statistics.median(l) 2 Пример №2 (excel) Медиана для ряда 1 2 3 4 5 6 7 8 9 10 = 5.5 ((5+6/2)) =MEDIAN(1;2;3;4;5;6;7;8;9;10) =PERCENTILE.INC(A1:A10; 0,5) =PERCENTILE.EXC(A1:A10; 0,5) Пример №3 (python) Дано: список зарплат рядовых медицинских сотрудников больницы (в тыс. руб.): 25, 17, 23, 18, 24, 23, 16, а также зарплата главврача – 85 и его заместителя – 50. Каков средний уровень зарплаты в больнице? Согласно среднему арифметическому, средняя зарплата по больнице – 31,2 тыс. рублей. Если же мы посчитаем вместо среднего арифметического медиану, то получим 23 тыс. рублей. Что, по-вашему, ближе к правде? Пример расчет в python: >>> import statistics >>> l = [25, 17, 23, 18, 24, 23, 16, 85, 50] >>> statistics.mean(l) 31.22222222222222 >>> statistics.median(l) 23 Наглядно между какими значениями находится среднее (23) и медиана (31): 16 17 18 23 23 24 25 50 85 В случае же отклонения распределения от нормального закона среднее значение использовать некорректно, так как оно является слишком чувствительным параметром к так называемым «выбросам» — нехарактерным для изучаемой выборки,слишком большим или слишком малым значением (рис. 2). В этом случае для характеристики центральной тенденции в выборке должен применяться другой параметр — медиана. Медиана — это значение признака, справа и слева от которого находится равное число наблюдений (по 50%). Этот параметр (в отличие от среднего значения) устойчив к «выбросам». Заметим также,что медиана может использоваться и в случае нормального распределения — в этом случае медиана совпадает со средним значением.
Рекурсия – в простом случае реализации вызов из функции самой функции. В общем случае. Пример реализации рекурсии описан в статье Python, пример оценки сложности в Оценка сложности алгоритма (асимптотическая оценка, оценка Big O)
Использовать рекурсию нужно аккуратно, зачастую задача прекрасно решается без нее. Рекурсия в общем случае более накладная операция по памяти см. в Оценка сложности алгоритма (асимптотическая оценка, оценка Big O). Я ее использовал для построителя топологии (запросы в базу для построения вниз по дереву графа) и binary search (поиск производительности), но к примеру, расчет факториала (ниже) легко реализуется за счет for + range (с рекурсией же вообще не работает на 1 млн. числах, в то числе с выкручиванием recursion depth sys.setrecursionlimit(xxx) падает с Segmentation fault: 11). Я тем более не говорю про определение является ли палиндромом строка, что можно реализовать сравнением массивов (деление на 2 и reverse перед сравнением).
При этом не стоит всегда выбирать итеративное решение вместо реркурсии, даже если оно есть – рекурсивное решение может быть значительно сложнее для реализации, а одинаковая потенциальная асимптотика в сравнении с итеративным решением + более простой код зачастую перевешивают минусы рекурсии.
Кроме того pay attention:
Для полноты картины обязательно надо упомянуть о борьбе с рекурсией. Зачем же с ней бороться? Повышается производительность. Но это не значит, что с ней просто необходимо бороться, ведь применение рекурсии очевиднее, проще и приятнее, чем итерационные варианты.
Последовательность/ряд Фибоначчи – частый вопрос на собеседованиях. Элемент равен сумме двух предыдущих N = (N-1)+(N-2). Соотношение смежных элементов около 0.61 (близко к золотому делению/сечению). Пример расчета числа и дерево вызовов есть в статье Python, пример оценки сложности в Оценка сложности алгоритма (асимптотическая оценка, оценка Big O)

Пузырьковая сортировка – базовая сортировка со сложностью O(n^2), популярный вопрос на собеседованиях. Почти все другие алгоритмы сортировки более эффективны (подробнее в оценке сложности). Принцип работы – в каждую итерацию мы гарантированно определяем «пузырек» в виде максимального элемента и перемещаем его вправа. Количество итераций в итоге не более чем N^2 (с дополнительным вычитанием последнего элемента). Пример реализации есть в статье Python, пример оценки сложности в Оценка сложности алгоритма (асимптотическая оценка, оценка Big O)
Алгоритм состоит из повторяющихся проходов по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется перестановка элементов. Проходы по массиву повторяются N-1 раз или до тех пор, пока на очередном проходе не окажется, что обмены больше не нужны, что означает — массив отсортирован. При каждом проходе алгоритма по внутреннему циклу очередной наибольший элемент массива ставится на своё место в конце массива рядом с предыдущим «наибольшим элементом», а наименьший элемент перемещается на одну позицию к началу массива («всплывает» до нужной позиции, как пузырёк в воде — отсюда и название алгоритма).

Быстрая сортировка на основе рекурсии (quick sort)
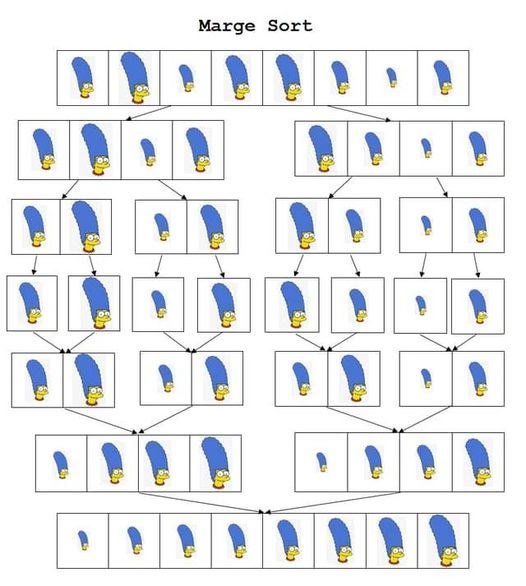
Сортировка рекурсивным слиянием (merge sort; recursive sorting algorithm) с двоичным делением
Шифр Цезаря – Решения задач с ним требуют деления с остатком – к текущему номеру символа прибавляется или вычитается сдвиг, из результата извлекается остаток деления на длину алфавита, что является номером нового символа. Теория в словаре, примеры решений в алгоритмах.
