Алгориртмы и структуры данных, оценка сложности алгоритмов (асимптотическая оценка, оценка Big O)

Почему алгоритмы это важно

Яндекс в курсе “Подготовка к алгоритмическому собеседованию” (я много раз ссылался на этот курc ниже, подкрепляя аргументацию или конспектируя новую ин-ию):

• • - Насколько кандидат умеет оценивать алгоритмическую и пространственную сложность кода. На очень больших объёмах данных, обрабатываемых в FAANG, даже небольшая разница в асимптотике может разделять рабочее решение и решение, которое не отработает за несколько лет.
    - Разработчик, знающий алгоритмы и структуры данных, может оценивать эффективность кода, в том числе в рабочих задачах и при проведении код-ревью.
    - Знание специфики разных структур данных помогает понимать их плюсы, минусы и условия применимости, выбирать правильные решения и поэтому писать более эффективный код.
    - Решение алгоритмических задач улучшает навык написания чистого кода. В них нет противоречивых требований продуктовой логики, некорректных входных данных, «магии», скрытой за фреймворками и вызовами внешних API. Поэтому почти для любой задачи на алгоритмы можно написать аккуратное, понятное, лаконичное и при этом эффективное решение.
    - Алгоритмы не устаревают. Они не привязаны к конкретным технологиям или техническому стеку, поэтому полученные знания и навыки будут актуальны до тех пор, пока люди не перестанут писать код.

Алгоритмическое интервью

К алгоритмическим собеседованиям нужно готовиться, поскольку это редко встречается в повседневной работе разработчика.

Стандартный формат:

1. 1. 2-3 задачи на 45-60 мин
   2. ключевое – решение задачи в условиях “ограничений” ((Решить задачу — значит без использования внешних источников за определённое время обсудить и написать на реальном языке программирования достаточно производительное решение без логических ошибок, при этом не имея возможности запускать код. Это — главное.))

В общем случае справедливо следующее

План подхода к решению задач ((В случае сомнений всегда спрашивайте у интервьюера.))

1. 1. общаемся ((Интервьюер рассказывает условие задачи. В нём может намеренно не хватать важных вводных, потому что ожидается, что кандидат это заметит и спросит. Уточняет ли кандидат параметры задачи? В реальности редко встречаются команды, где в разработку передаётся идеальное, подробно расписанное задание. Как правило, его требуется уточнять с заказчиком или руководителем.))
      1. уточнить правильно ли понял задачи – После вводной части интервьюер формулирует задачу. Сейчас самое важное — разобраться в условии. Лучше всего подойдёт такой способ: перескажите условие своими словами и спросите, правильно ли вы всё поняли. При необходимости можно попросить интервьюера повторить задачу или ответить на вопросы.
      2. уточнить входные данные
         1. требуется ли input validation на заведомо некорректные данные на входе – чаще всего не нужно, но можно уточнить
         2. В зависимости от задачи может потребоваться прояснить формат входных данных. Какие структуры будут поступать на вход функции, которую вам нужно реализовать? В ответ интервьюер может спросить, какой формат вам был бы наиболее удобен. Об этом сто́ит подумать. Во-первых, так вам будет проще решать задачу. Во-вторых, вопрос о формате — упрощённая проверка архитектурного навыка, то есть того, насколько хорошо вы можете проектировать интерфейсы. Выясните ограничения. Есть ли условия для входных данных? Допустим, вам нужно что-то сделать с массивом чисел. Тогда важно понять, о каких числах идёт речь: целых или с плавающей точкой. А может быть, гарантируется, что они будут неотрицательными. 
      3. тестовые данные – написать тестовые данные – int/out: f([1,2,3,3]) = 2
         1. Придумайте тестовый пример. Это должен быть хороший общий тест. В следующем уроке мы подробно расскажем, что это такое. Пока можно считать, что это тест, на котором можно будет проверить, что идея и решение в целом рабочие. Пользуясь этим примером, подумайте, как достичь нужного результата. Удобнее всего делать это на листочке бумаги или доске.
         2. для некоторых задач это сверх критично – напр. смотри ниже задачу на пересечение двух отрезков Выясните ожидаемое поведение на краевых случаях. Можно сделать это устно («Что должна выдавать программа или функция, если входной массив пуст?») или через тест-кейсы. Если решили выписать тест-кейсы, делайте это максимально просто, хоть комментарием в коде. Использовать реальную библиотеку для тестирования необязательно, поэтому нужен самый быстрый вариант.
         3. включая стандартные и краевые/специальные/edgecase случаи для последующих тестирований (нужно соблюдать баланс – слишком много тестов тоже плохо) – Выясните ожидаемое поведение на краевых случаях. Можно сделать это устно («Что должна выдавать программа или функция, если входной массив пуст?») или через тест-кейсы. Если решили выписать тест-кейсы, делайте это максимально просто, хоть комментарием в коде. Использовать реальную библиотеку для тестирования необязательно, поэтому нужен самый быстрый вариант.
         4. в итоге всегда перед глазами иметь представление с чем работаем (тестовые данные) – итак, к этому моменту нужно хорошо понимать, что от вас требуется. Если что-то важное осталось непонятным — обязательно выясните, задавая вопросы. Главное — не базироваться на неозвученных предположениях. Иначе можно решать не ту задачу, которую нужно, а это почти гарантированный путь к провалу. Аналогия с промышленной разработкой должна быть очевидна: если сделать не то, что нужно заказчику, потом придётся много переделывать.
      4. уточнить параллельно требования к алгоритму в процессе описания тестовых данных – проверка ТЗ, напр. в случае in-place уточнить можно ли доп. переменные (не массивы) заводить
      5. Итак, к этому моменту нужно хорошо понимать, что от вас требуется. Если что-то важное осталось непонятным — обязательно выясните, задавая вопросы. Главное — не базироваться на неозвученных предположениях. Иначе можно решать не ту задачу, которую нужно, а это почти гарантированный путь к провалу.
   2. придумать возможный алгоритм, если он не подходит (об этом отдельно спрашивать нужно – напр. подходит ли рекурсивное решение) – потенциально сравнить/описать альтернативы и их плюсы/минусы
      1. Кандидат обсуждает с интервьюером идеи решения. С первого раза решение может быть неправильным или медленным — это нормально, интервьюер на это укажет и предложит ещё подумать. При необходимости даст подсказку.))
         1. Придумайте какое-нибудь корректное решение. Даже если оно очень простое — расскажите его интервьюеру. Оцените время работы и затраты по памяти и, если думаете, что можно решить задачу быстрее, скажите об этом. Так вы покажете интервьюеру, что поняли задачу, можете придумывать простые решения и оценивать их эффективность. Скорее всего, нужно будет придумать более быстрое решение, поэтому не тратьте много времени на простое.
      2. Интервьюер зачастую помогает найти хорошее решение. Как раз на этом этапе нормально, если вы сразу не можете придумать оптимальное решение и рассуждаете вместе с интервьюером. Он должен понимать ход ваших мыслей и задавать наводящие вопросы так, чтобы, с одной стороны, помочь, а с другой — не раскрыть решение с первой же подсказки.
      3. Не нужно сразу бросаться в бой и пытаться запрограммировать то, что по какой то причине не подошло при обсуждении (напр. алгоритм плох т.к. асимптотически слишком сложен или использует запрещенные функции) – может быть риск потери времени и негатив “взялся за бесполезное программирование”
      4. Не факт, что от вас ожидают именно оптимального решения. Например, в некоторых задачах допускается решение как за O(n)O(n)O(n), так и за O(nlog⁡n).O(n \log n).O(nlogn). Но обязательно сверьтесь с собеседующим.
      5. Старайтесь, чтобы логика кода была максимально прямолинейной. В нём проще избежать ошибок. «Запахи»‎ плохого кода:
         1. Чрезмерно высокая вложенность.
         2. Много if, особенно вложенных, особенно внутри циклов: проследить логику такого кода практически невозможно.
         3. Неясно, что является состоянием и как оно изменяется.
         4. Старайтесь избегать copy-paste. Дублировать похожий код не сто́ит. Но и обобщать не сильно похожие куски не следует.
   3. реализовать, если не подходит – вернуться к п.3
      1. При использовании встроенных в язык средств (напр. структур данных Counter, SourtedList, OrderedDict) нужно понимать как они работают – вычислительная сложность, сложность по памяти, какие могут быть проблемы, если такого понимания нет – лучше реализовать самому алгоритм
      2. В общем случае не рекомендуется использовать однобуквенные имена переменных или имена, отличающиеся одним символом. При этом так же справедливо и обратное – Давайте функциям и переменным короткие и осмысленные имена. Слишком длинные имена скрадут у вас много времени.
      3. Чтобы придумать решение, в первую очередь нужно знать стандартные алгоритмы и структуры данных. Какими-то функциями стандартной библиотеки пользоваться можно и даже нужно. Например, если для решения требуется отсортировать данные, скорее всего, нужно использовать сортировку из стандартной библиотеки, а не писать свою. Если не знаете, можно ли использовать тот или иной инструмент, — спрашивайте у интервьюера.
      4. Код должен логически работать, а вот на мелкие опечатки обычно закрывают глаза, при этом именно безобидные опечатки, если код логически стал неправильным – это критично, перечисленные важно не допускать
         1. Ошибка в индексах: arr[i + 2] вместо arr[i + 1]. Сюда же относятся ситуации, когда происходит выход за пределы массива и программа завершается с ошибкой.
         2. Иногда неточность при работе с индексами может привести к тому, что программа на некоторых тестах будет уходить в бесконечный цикл.
         3. Ошибка в знаке: i = i + 1 вместо i = i – 1.
         4. Вызов метода с семантикой или асимптотикой, отличной от ожидаемой.
         5. Неправильный тип или операция с числовой переменной.
      5. Специальные случае зачастую не требуют отдельной обработки в задаче, появление такой обработки (if-чиков), когда это не нужно (решается изменением/доработкой в общем обработке) и не покрывает все проблемные сценарии, является по сути костылем и багом кода! При этом пустой массив на входе обрабатывать отдельным if вначале функции (не в цикле) не возбраняется. Наконец, алгоритмическое собеседование позволяет показать, насколько кандидат способен разобраться в причине бага и исправить код. Хорошо, когда исправлена причина. Но бывает и так, что вместо этого ставится дополнительная проверка, а по сути «заплатка». Она приводит к запутанному коду и не покрывает все ломающиеся случаи.
   4. Протестировать на тестовых данных,  причем ((код обычно не запускается – пишется на доске или редакторе без возможности запуска))
   5. Если вы понимаете, что всё делаете быстро, и точно знаете, как улучшить свой код, скажите об этом интервьюеру. Возможно, у него больше нет для вас задач и вы сможете заняться рефакторингом.

Что обычно не нужно

1. 1. 1. В языке Python мы не будем указывать типы. На собеседованиях вам тоже не нужно будет этого делать.
      2. Язык программирования зачастую не важен – На собеседовании пишите код на том языке, который вы знаете лучше всего, чтобы не запутаться в объявлении функций или стандартных структур данных. 
      3. Не нужно делать input validation, если это заведомо не требуется – приходящие данные корректны, при этом пустой массив вместо массива с числами скорее корректный case и его нужно проверять/обрабатывать ((Предполагается, что коду кандидата поступают на вход корректные данные. 1) нужно считать, что придёт именно массив целых чисел, а не писать обобщённый код; 2) не надо проверять, не пришёл ли null вместо массива; 3) массив вполне может быть пустым — это не противоречит условию.))
      4. Обычно решение задачи не требует много кода – Задачу можно решить простым и понятным кодом не более чем на 30 (очень редко — больше) строк. 
      5. Специфические алгоритмы не проверяют – от разработчика не ожидается знаний сложных и узкоспециализированных алгоритмов и структур данных. Предполагается, что если он уверенно владеет базой, при столкновении с новой задачей он уже будет знать, что и где искать, и сможет придумать решение. Графы, динамическое программирование и деревья поиска в яндексе спрашивают редко (обычно только когда позиция требует “жестких” алгоритмов).
      6. Проверяют на алгоритмическое мышление, а не на знание спец. либ языка – Для решения достаточно знаний языка и его стандартной библиотеки. Если вы придумали, как решить задачу в несколько строк с помощью внешней библиотеки, можете коротко рассказать идею интервьюеру. Так вы покажете широту своего кругозора. Но не тратьте на это больше пары минут — скорее всего, интервьюер попросит вас написать решение без внешней библиотеки. Не предполагается, что вы помните всю стандартную библиотеку наизусть, но базовые вещи кандидат должен делать уверенно.
      7. Задачи-головоломки («‎почему люки круглые?») или задачи на математику уже давно не даются. При этом вполне возможны задачи, где нужно прийти к какой-нибудь несложной, но не самой очевидной идее.
      8. СУБД-СЕТЬ – Задачи не требуют взаимодействия с внешними ресурсами, такими, как СУБД или сеть. В редких случаях может понадобиться работать со стандартными потоками ввода и вывода.
      9. EDGE-CASE – В таких задачах не требуется разбора большого количества граничных случаев, также называемых корнер-кейсами.
      10. ПОТОКИ – Если явно не сказано обратное, предполагается, что ваш код будет запускаться в одном потоке.
      11. КОДИРОВКИ –  Если в задаче требуется работать со строками, то обычно можно считать, что алфавит ограничен ASCII-символами, то есть не нужно разбираться с кодировками.
      12. Алгоритмическое интервью проходит в режиме сильно ограниченного времени, поэтому никто не ожидает от кандидата кода продакшен-качества.

Структуры данных

• Сложность по памяти во многом вопрос правильно выбранной структуры данных.
• Пример интересной структуры данных – кольцевой буфер
• Индексы БД – прекрасный пример повышения производительности за счет правильно выбранной структуры данных
  • создаем доп. таблицу за счет которой осущпствляем более быстрый lookup из-за того, что она упорядочена – поиск в отсортирорванном массиве быстрее, чем в неотсортированном
  • в минусах, поэтому индексы используют не всегда и не для всех столбцов
    • пересчет индексов (учет в индексной таблице изменений) при изменении таблиц – замедляется insert данных в таблицу
    • создание доп. структуры – это расходы по памяти

Пример выбора структуры данных от ТЗ

Множество (Set) — структура данных, которая позволяет достаточно быстро (в зависимости от реализации) применить операции add, erase и is_in_set. Но иногда этого не достаточно: например, невозможно перебрать все элементы в порядке возрастания, получить следующий / предыдущий по величине или быстро узнать, сколько элементов меньше данного есть в множестве. В таких случаях приходится использовать Упорядоченное множество (ordered_set). 

В языке c++ есть структура std::set, которая поддерживает операции изменения, проверку на наличие, следующий / предыдущий по величине элемент, а также for по всем элементам. Но тут нет операций получения элемента по индексу и индекса по значению, так что надо искать дальше (индекс элемента — количество элементов, строго меньших данного)

И решение находится достаточно быстро: tree из pb_ds. Эта структура в дополнение к возможностям std::set имеет быстрые операции find_by_order и order_of_key, так что эта структура — именно то, что мы ищем.

сложность алгоритмов

Асимптотическая оценка Анализ сравнения затрат времени алгоритмов, выполняемых решение экземпляра некоторой задачи, при больших объемах входных данных, называется асимптотическим. Алгоритм, имеющий меньшую асимптотическую сложность, является наиболее эффективным. В асимптотическом анализе, сложность алгоритма – это функция, позволяющая определить, как быстро увеличивается время работы алгоритма с увеличением объёма данных.

Big O показывает верхнюю границу зависимости между входными параметрами функции и количеством операций, которые выполнит процессор.

https://www.youtube.com/watch?v=cXCuXNwzdfY

Асимптотическая оценка/оценка Big O – оценка сложности алгоритма (скорости/эффективности/производительности) в виде количества выполняемых операций с увеличением объема обрабатываемых данных.

Три важных момента на мой взгляд:

1. 1. По результату различный округлений 4N -> N, 1/2N -> N (что корректно с точки зрения решаемой задачи оценки алгоритма с ростом данных) одинаковые по расчетной сложности алгоритмы по фактической скорости на одном массиве данных могут сильно отличаться (см. пример duplicate_detection функций в статье Python).
   2. Одна и та же функция может иметь разную сложность, в зависимости от сценария ее использования, нужно отталкиваться от худшего именно в вашем сценарии использования; хорошие примеры pop и enumerate Python, много других примеров (average, worst case) в Таблицах с известными стоимостями для стандартных функций Python.
   3. Оценку по моему мнению нужно в первую проводить тогда, когда есть соответствующие потребности в “больших данных” потому что (В промышленной разработке важно именно понимать реальную и допустимые асимптотики участков кода. Необязательно оптимизировать места, где нагрузки маленькие. Если допустимое решение намного проще, лучше использовать именно его, ведь оно проще поддерживается.):
      1. алгоритм, решающий задачу на больших данных может решать задачу хуже на малой выборке данных, а малая выборка при этом может составлять большую/единственную часть потенциальных данных/”запросов”
      2. универсальный алгоритм, решающий задачу оптимально на любой выборке (большой или малой) может быть значительно более сложно реализуем/читаем или не реализуем вообще или потреблять большее количество ресурсов или иметь другие существенные недостатки (напр. долгая время на инициализацию, как с префиксными деревьями в DPDK, требующих значительное время на инициализацию при изменении)
   4. Нужно оценивать все функции в контексте бизнес задач, в каких функциях наиболее важна асимптотика – какие то реализации могут ускорять одни операции, а другие реализовывать хуже (яндекс в курсе “Подготовка к алгоритмическому собеседованию”).

Второе решение намного быстрее находит лучшие работы. Возможно, его стоит предпочесть, если у нас больше нет никаких дополнительных данных. Но может оказаться, что этот топ нужно пересчитывать раз в сутки, чтобы не было накрутки голосов. При этом поток реакций на работы ожидается большой. Тогда первое решение предпочтительнее, так как оно максимально быстро обрабатывает основной поток запросов, при этом не создавая критически медленных частей. В реальной разработке зачастую не всегда существует единственно правильное решение. Поэтому разработчику нужно выяснить требования, оценить сильные и слабые стороны возможных альтернатив и выбрать наилучшую. 

И дальше в общем, но тоже крайне важно (о сравнении алгоритмов):

Определить кратчайший путь, выбрать необходимое подмножество объектов, найти наилучшее совпадение строк — каждую из этих задач можно решить несколькими разными способами. Все они дадут одинаковый результат, но один вариант окажется самым простым в реализации, другой — более эффективным, а третий — максимально быстрым, но при этом будет использовать много оперативной памяти.

Алгоритмическая подготовка позволяет разработчику понимать корректность своего кода. То есть убеждаться в том, что решение в принципе даёт правильный ответ. Рассмотрим простейшую задачу — поиск одного элемента в массиве:
1) Простой проход по массиву будет оптимальным решением.
2) Сложить все элементы в хеш-таблицу и проверить существование элемента будет корректным, но не оптимальным решением — оно -требует много дополнительной памяти.
3) Бинарный поиск по массиву будет некорректным решением, если массив не отсортирован.

Наиболее встречаемые вариации сложности

Сложность по памяти (memory complexity)

In-place algorithm – алгоритм, не использующий дополнительную память/структуры данных для своей работы.

In computer science, an in-place algorithm is an algorithm which transforms input using no auxiliary data structure. However, a small amount of extra storage space is allowed for auxiliary variables.

Сложность по памяти не учитывает объем данных на входе в алгоритм, она нужна для расчета дополнительной памяти, которую алгоритм задействует для своей работы при работе с исходными данными на входе. Именно сложность по памяти во многом вопрос правильно выбранной структуры данных. Сложность по памяти нужно рассматривать/расчитывать отдельно, для функции итерации (с вложениями или без вложений) например она O(1), а не O(N); для последовательности Фибоначчи она O(N), а не O(N^2). Если говорить в среднем:

• • Для нерекурсивных функций сложность по памяти O(1) ((если не создается доп. структур, зависимых от N – см. пример пример duplicate_detection функций в статье Python))
  • Для рекурсивных функций сложность по памяти O(N)

Примеры расчета вычислительной сложности (TIME complexity)

• Таблицы с известными стоимостями для стандартных функций Python.
• Вторая таблица (напр. в ней есть reverse, в отличии от первой) 
  • Sort
    • O(n log n)
  • Enumerate
    • Initialization: O(1)
    • Returning the next element: O(1)
    • Returning all elements: n * O(1)
  • Dictionary
    • Worst case for all operations: O(n)
    • Average case: 
      • Get, Set, Delete: O(1)
      • Copy, Iterate: O(n)
    • The Average Case times listed for dict objects assume that the hash function for the objects is sufficiently robust to make collisions uncommon.
    • Note that there is a fast-path for dicts that (in practice) only deal with str keys; this doesn’t affect the algorithmic complexity, but it can significantly affect the constant factors: how quickly a typical program finishes.
  • POP
    • Pop last O(1)
    • Pop intermediate O(n)
  • Slice
    • Get O(k) – по количеству элементов в запросе [0:3] = 3
    • Del O(n) – по количеству элементов в массиве
    • Set O(k+n) – сумма добавляемых и существующих элементов
  • Reverse – O(n)
  • Split and Strip
    • O(n)
  • Counter
    • O(n)

Расчет сложности часто делается “на глаз” визуализируя количество операций, точный математический расчет может требовать длительного времени. Пример – в библиотеке Python Sortedcontainers большая часть “Runtime/Time complexity” показана с меткой “approximate”. Совсем грубо все операции в нем O(logN).

Константная сложность O(1) – сложность не зависит от входных данных, например

• • на входе в функцию фиксированный набор данных
  • если весь объем информации перенести (перевезти) физически, например на самолете

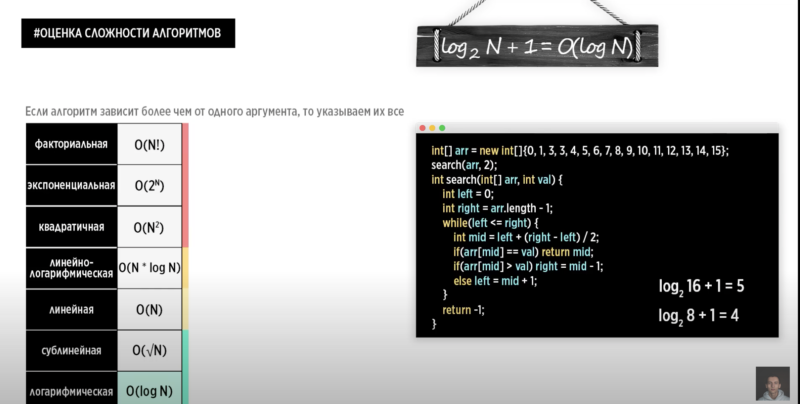
Логарифмическая сложность O(log N)

• Бинарный поиск (binary search/дихотомия) в отсортированном массиве – для алгоритма, где на каждой итерации берется половина элементов, сложность будет включать O (log N) в формуле сложности (например N log N, и т.п.).
  • Берем середину массива
  • Число меньше середины идем в левый подмассив, больше — в правый
  • Повторяем тоже самое для подмассива
  • Конец, когда нашли искомое или длина массива станет 1

Сублинейная сложность O(sqr N)

Линейная сложность O(N) – линейный рост данных приводит к линейному росту вычислений (10 переменных – 10 прохождений кода)

• • Итерации итерации без вложений
  • Простые рекурсивные функции
  • Преобразование list в set (On time complexity,  On memory complexity хоть и доп структура != list, она зависит от размера list)
    • Iterating over a list is O(n) and adding each element to the hash set is O(1), so the total operation is O(n).
    • set() is essentially iterating over the list and adding each of those elements to a hash table.
    • The important part is the call to set, which has to allocate a data structure with n new references, one per element in list_var, so the space complexity is O(n).
  • При передаче данных файлов по сети: Если считать файлы как биты, то при передаче данных через Интернет получается, что чем больше бит, тем больше времени требуется для передачи.

# Рекурсивная функция
int sum(int n) {
  if (n == 1) return 1;
  return n + sum(n - 1);
}

# Использование цикла с вызовом вспомогательной функции
int pairSumSeq(int n) {
  int sum = 0;
  for (int i = 0; i < n; i++) { 
    sum+= pairSum(i, i+1);
  }
}

int pairSum(int a, int b) { // Сложность: O(1)
  return a + b;
}

Сложность O(N + K)

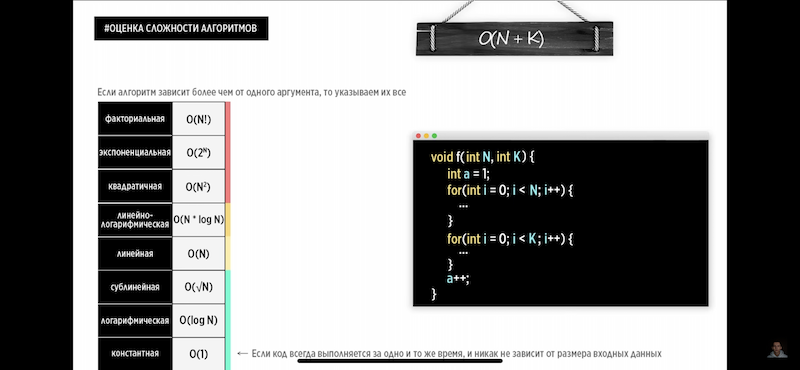
# последовательность действий — сложение
for (int a : arrA) {
  print(a);
}

for (int b : arrB) {
  print(b);
}

Линейно-логарифмическая сложность – напр. O(N log N)

Пример быстрая сортировка (quick sort) на основе рекурсии, пример реализации смотри в python. Сложность (думаю) аналогична стандартному sort – O(NlogN). Она явно больше линейной т.к. проход по циклу делается каждую итерацию, но меньше квадратичной т.к. вложенных проходов меньше – сопоставимо с бинарным поиском, сложность которого O(logN).

Сложность O(N * K) 

# повторение повторений ((с разной длинной массивов N и K иначе см. квадратичную) — умножение
for (int a : arrA) {
  for (int b : arrB) {
    print(a + ", " + b);
  }
}

Квадратичная/кубическая сложность O(N^2) и O(N^3)

• • Вложенные итерации
  • Частный случай – пузырьковая сортировка

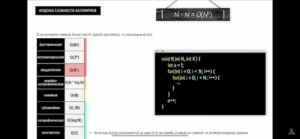
Экспоненциальная сложность O(2^N)

• Несколько рекурсивных вызовов

• Частный случай – последовательность Фибоначчи, в примерах деревья вызовов для числе 5 и 6 (recursive call tree).

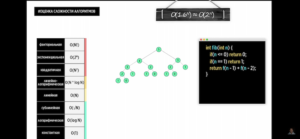
Факториальная сложность O(N!)

• Перестановки всех элементов массива

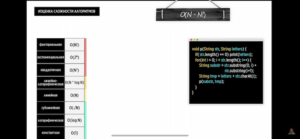
Решение разных задач, в том числе на алгоритмы

Еще пример от яндекса – кратко рейтинги участников, возврат лучших работ по лайкам. Задача расписана в двух статьях т.к. представляет интерес как с точки зрения статьи Coding: Python заметки, так и с точки зрения статьи Алгориртмы и структуры данных, оценка сложности алгоритмов (асимптотическая оценка, оценка Big O)

Решение на базе сортировки:

• • get_best_works – сама задача по возврату лучших работ решается простой сортировкой и reverse (чтобы старшие элементы, имеющие больший рейтинг были первыми). Сложность O(NlogN) по сложности sort, reverse имеет сложность O(N), enumerate имеет сложность O(1). При этом сортировка+reverse могут быть заменены на QuickSelect алгоритм, имеющий сложность O(N).
  • (dis)like – O(1) по сложности dictionary set

class Competition:
    def _change_score(self, participant_id, change):
        self._scores[participant_id] += change

    def __init__(self, participant_count):
        self._scores = [0] * participant_count

    def like(self, participant_id):
        self._change_score(participant_id, 1)

    def dislike(self, participant_id):
        self._change_score(participant_id, -1)

    def get_best_works(self, count):
        scores_ids = [(value, id) for id, value in enumerate(self._scores)]
        scores_ids.sort(reverse=True)
        return [id for _, id in scores_ids[:count]]

Решение на базе сортировки:

• • get_best_works – сама задача по возврату лучших работ решается той же сортировкой, только реализуемой на базе специальной структуры, которая поддерживает сортировку элементов SortedList/SortedSet (initial_frequencies используется для создания sortedset и не более; scores используется для хранения значения like; sortedset как доп структура scores для быстрой работы get_best_works) и вывод через slice нужного количества последних элементов, имеющих наибольшее количество Like. Сложность O(K) по сложности slice в SortedSet.
  • (dis)like – O(logN) по сложности операций add, remove

from sortedcontainers import SortedSet

class Competition:
    def __init__(self, participant_count):
        self._scores = [0] * participant_count
        initial_frequencies = [(0, id) for id in range(participant_count)]
        self._ordered_works = SortedSet(initial_frequencies)

    def _change_score(self, participant_id, change):
        old_participant_stat = (self._scores[participant_id], participant_id)
        self._ordered_works.remove(old_participant_stat)
        self._scores[participant_id] += change
        new_participant_stat = (self._scores[participant_id], participant_id)
        self._ordered_works.add(new_participant_stat)

    def like(self, participant_id):
        self._change_score(participant_id, 1)

    def dislike(self, participant_id):
        self._change_score(participant_id, -1)

    def get_best_works(self, count):
        return [id for (_, id) in self._ordered_works[-count:][::-1]]

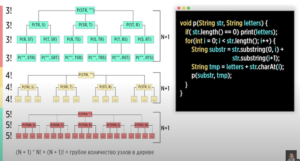
Задача по правильные скобочные последовательности – “дано натуральное число N, требуется вывести все правильные скобочные последовательности длины 2N” – по сути генератор скобок, который принимает на входе общее количество скобочных последовательностей (открытых и закрытых скобок). Решить задачу с помощью чего то кроме рекурсии достаточно сложно (пробовал с помощью циклов; потенциально требуется использование доп. структуры типо стека), да и с рекурсией есть различные подводные камни при решении (в видео). Как обычно с рекурсиями: Как работает рекурсия проще всего понять по коду ниже c print (или интерактивно в режиме дебага) и в виде деревьев вызовов (напр. для расчета числа Фибоначчи для 5).

def bracket_generator(line, bropen, brclosed, n):
    if len(line) == 2 * n:
        print(line)
        return
    if bropen < n:
        bracket_generator(line + "(", bropen + 1, brclosed, n)
    if brclosed < bropen:
        bracket_generator(line + ")", bropen, brclosed + 1, n)


bracket_generator("", 0, 0, 3)

 # time complexity O(N*LOGN), memory complexity O(N)
def is_anagram1(line1: str, line2: str) -> bool:
    """check two str and return anagram second from
    first or not"""
    return sorted(line1) == sorted(line2)

# time complexity O(N), memory complexity O(N)
def is_anagram2(line1: str, line2: str) -> bool:
    """check two str and return anagram second from
    first or not"""
    return Counter(line1) == Counter(line2)

# time complexity O(N), memory complexity O(1)
def is_anagram3(line1: str, line2: str) -> bool:
    """check two str and return anagram second from
    first or not"""
    line1_dict = dict()
    line2_dict = dict()
    for item in line1:
        line1_dict[item] = line1_dict.get(item, 0) + 1
    for item in line2:
        line2_dict[item] = line2_dict.get(item, 0) + 1
    print(line1_dict)
    print(line2_dict)
    return line1_dict == line2_dict

# time complexity O(N), memory complexity O(1)
def is_anagram(line1: str, line2: str) -> bool:
    """check two str and return anagram second from
    first or not"""
    line1_dict = defaultdict(int)
    line2_dict = defaultdict(int)
    for item in line1:
        line1_dict[item] = line1_dict[item] + 1
    for item in line2:
        line2_dict[item] = line2_dict[item] + 1
    return line1_dict == line2_dict


l = "asdasdg"
l2 = "dsadsa"
l3 = "dsaasd"
print(is_anagram(l, l2))
print(is_anagram(l2, l3))
>>>
False
True

 # time complexity O(N), memory complexity O(1)
def max_bin_len(bin_list: list) -> int:
    """find max bin len"""
    b_max = 0
    b_current = 1
    prev_val = ""
    for bin_val in bin_list:
        if prev_val == bin_val:
            b_current += 1
            b_max = max(b_current, b_max)
        else:
            b_current = 1
        #OLD if b_current > b_max:
        #OLD     b_max = b_current
        prev_val = bin_val
    return b_max


l = [0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0]
print(max_bin_len(l))
l = [0, 0, 0, 0, 0, 0, 0]
print(max_bin_len(l))


>>>
7
7

bank_money = [ 1000, 1000, 500, 500, 100, 5000, 100, 100 ]
user_money = 1300

def min_coin_withdrawal(bank_money: int, user_money: int) -> list:
    withdrawal = []
    # сортируем наличные в банкомате по убыванию
    descending_bank_money = list(reversed(sorted(bank_money)))
    while user_money != 0:
        # отбрасываем купюры больше запрашиваемой суммы
        descending_bank_money = list(banknote for banknote in descending_bank_money if banknote <= user_money)
        banknote = descending_bank_money[0]  # берем первую купюру из списка
        user_money = user_money - banknote
        withdrawal.append(banknote)
    return withdrawal

print(min_coin_withdrawal(bank_money, user_money))


>>>
[1000, 100, 100, 100]

True при обнаружении повторений в массиве чисел, False иначе.

'''test function'''
#!/usr/bin/env python3
# -*- coding: utf-8 -*-

from collections import Counter

# time complexity O(N), memory complexity O(N)
def duplicate_detection(potential_duplicates: list[int]) -> bool:
    '''Detecting dups'''
    service_list = []
    for potential_duplicate in potential_duplicates:
        if potential_duplicate in service_list:
            return False
        service_list.append(potential_duplicate)
    return True

# time complexity O(N) (3N: set, 2len), memory complexity O(N)
def duplicate_detection_old1(potential_duplicates: list[int]) -> bool:
    '''Detecting dups'''
    return len(potential_duplicates) > len(set(potential_duplicates))

# time complexity O(N() (4N: counter, sorted, reversed, iteration), memory complexity O(N)
def duplicate_detection_old2(potential_duplicates: list) -> bool:
    '''Detecting dups'''
    array = Counter(potential_duplicates)
    for count in reversed(sorted(array.values())):
        if count > 1:
            return False
        if count == 1:
            return True

l = [ 1,2,1,3,4 ]
print(duplicate_detection(l))
l2 = [ 1,2,3,4.5 ]
print(duplicate_detection(l2))


>>>
False
True

Удаление дублей в отсортированном массиве.

1. 1. Самое простое преобразовать в set, с точки зрения Алгориртмы и структуры данных, оценка сложности алгоритмов (асимптотическая оценка, оценка Big O)
   2. Алгоритм ниже 1) требует меньше памяти – реализует так называемый in-place algorithm 2) потенциально быстрее (ему не нужно лукап делать по всему массиву для поиска дублей, только по следующим элементам). Но это решение использует pop не последнего элемента, вычислительная сложность pop в таком случае O(N), для последнего O(1).
   3. В общем случае всегда когда видим sorted list оптимальным будет решение с двумя указателями/pointer – в данном случае так и есть. По сути первый pointer отвечает за создание массива с нуля на основе существующего массива, а второй pointer отвечает за прохождение по первичному массиву и поиск в нем уникальных значений.

# time complexity O(N), memory complexity O(1)
def duplicate_deletion(potential_duplicates: list[int]) -> list[int]:
    '''deleting dups in sorted list'''
    pointer1 = 0
    pointer2 = 0
    while len(potential_duplicates) > pointer2+1:
        while len(potential_duplicates) > pointer2+1 and \
                potential_duplicates[pointer2] == potential_duplicates[pointer2+1]:
            pointer2+=1
        potential_duplicates[pointer1] = potential_duplicates[pointer2]
        pointer1+=1
        pointer2+=1
    return potential_duplicates[:pointer1]

# time complexity O(N), memory complexity O(1)
def duplicate_deletion_old(potential_duplicates: list[int]) -> list[int]:
    '''deleting dups in sorted list'''
    for k_pd, v_pd in enumerate(potential_duplicates):
        while len(potential_duplicates) > k_pd+1 and v_pd == potential_duplicates[k_pd+1]:
            potential_duplicates.pop(k_pd+1)
    return potential_duplicates

l = [ 1,1,1,2,3,4,5,6,6,6,6,7,8,89,100,100,100 ]
print(duplicate_deletion(l)) 


>>>
[1, 2, 3, 4, 5, 6, 7, 8, 89, 100]

рекурсия

Теория о рекурсии в Статистика и математика в IT (в том числе акцент на сомнительности ее использования везде), пример оценки сложности алгоритма в Оценка сложности алгоритма (асимптотическая оценка, оценка Big O)

Вызов из функции той же самой функции, простейший пример (завершается с защитой от петли – RecursionError: maximum recursion depth exceeded while calling a Python object):

def rec(txt: str) -> str:
  print(txt)
  rec(txt)

rec("10")

Пример рекурсии с выходом.

def rec(x: int = 0) -> int:
  print(x)
  if x < 10:
    rec(x + 1)

rec(5)

Расчет факториала с помощью рекурсии.

def fact(x: int = 1) -> int:
  if x == 1:
    return x
  return fact(x - 1) * x

print(fact(4))

Как работает рекурсия проще всего понять по коду ниже c print (или интерактивно в режиме дебага) и в виде деревьев вызовов (напр. для расчета числа Фибоначчи для 5).

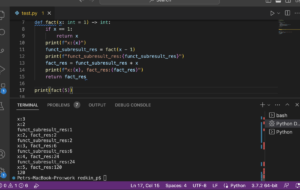
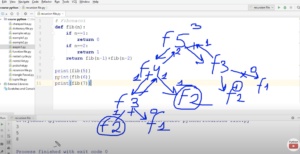
Альтернатива расчета факториала без использования рекурсии (не говоря про встроенную from math import factorial).

def fact_range(digit: int = 1) -> int:
  res = 1
  for x in range(1, digit+1):
    res = x * res
  return res

print(fact(5))

Сортировки

Пузырьковая сортировка в python (bubble sort)

Описание алгоритма в Статистика и математика в IT, пример оценки сложности в Оценка сложности алгоритма (асимптотическая оценка, оценка Big O). Скорость алгоритма ниже 16 минут (Core i5 2133 MHHz) на 100 тыс. рандомизированных чисел от -100 тыс до 100 тыс.

def bubble_sort(to_sort: list) -> list:
    for depth in range(len(to_sort)):
        for index in range(len(to_sort)-1-depth):
            if to_sort[index] > to_sort[index+1]:
                to_sort[index], to_sort[index+1] = to_sort[index+1], to_sort[index]
    return to_sort

array = [677, 234, 15, 222222, 3, 9, 2, 3, 6, 12, 234, 11, 1, -100, -234, -55, 123124, 444]
print(bubble_sort(array))


>>>
[-234, -100, -55, 1, 2, 3, 3, 6, 9, 11, 12, 15, 234, 234, 444, 677, 123124, 222222]

Быстрая сортировка на основе рекурсии (quick sort)

Основной принцип работы

– выбираем опорный элемент (с точки зрения кода проще всего первый или последний – индекс которого всегда будет в массиве),

– все элементы меньше него помещаем в группу “левых”, элементы старше в группу “правых”

– в каждой полученной группе так же выбираем опороный элемент и используем логику выше

– так доходим до единственного элемента, который будет опорный и схлопываем их (пустые списки отбрасываем)

Сложность O(NlogN). Подробнее в отдельной статье.

Скорость алгоритма менее 1 секунды (Core i5 2133 MHHz) на 100 тыс. рандомизированных чисел от -100 тыс до 100 тыс.

 def quick_sort(to_sort: list) -> list:
    if len(to_sort) <= 1:
        return to_sort
    base = to_sort[0]
    left = []
    right = []
    middle = []
    for val in to_sort:
        if val < base:
            left.append(val)
        elif val > base:
            right.append(val)
        elif val == base:
            middle.append(val)
    return quick_sort(left) + middle + quick_sort(right)

array = [677, 234, 15, 222222, 3, 9, 2, 3, 6, 12, 234, 11, 1, -100, -234, -55, 123124, 444]
print(quick_sort(array))


 >>>
[-234, -100, -55, 1, 2, 3, 3, 6, 9, 11, 12, 15, 234, 234, 444, 677, 123124, 222222]

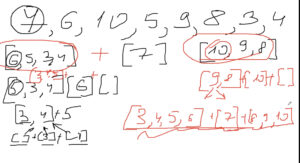
Быстрый выбор (QuickSelect)

Принцип работы похож на быструю сортировку – рекурсивно выбирается произвольный элемент, значения выше и ниже помещаются в отдельные группы с той лишь разницей, что группа равенства отдельная не создается.

Техническое описание.

The algorithm is similar to QuickSort. The difference is, instead of recurring for both sides (after finding pivot), it recurs only for the part that contains the k-th smallest element. The logic is simple:
1) If index of the partitioned element is more than k, then we recur for the left part. 
2) If index is the same as k, we have found the k-th smallest element and we return. 
3) If index is less than k, then we recur for the right part. 

This reduces the expected complexity from O(n log n) to O(n), with a worst-case of O(n^2).

Забавное описание на stackoverflow.

You walk into a gymnasium containing 200 children. It is September 8th, so you have a burning desire to find the 98th shortest child. You know that you could line them all up from shortest to tallest, but that would take forever. "I know", you think, "I could use QUICKSELECT!"

You walk out into the crowd, close your eyes, stick out your finger, and spin around three times. When you open your eyes, you are pointing directly at one of the children, Peter Pivot. You say, "Quickly! Everybody shorter than Peter, come stand over here. And everybody taller than Peter, go stand over there. If you're the same height as Peter, you can go into either group."

The children shuffle around, and soon they are standing in the two groups. You count and find 120 children in the shorter group, and 79 children in the taller group. You know the 98th shortest child must be in the shorter group, so you tell Peter and the 79 taller children to sit in the bleachers.

You again close your eyes, stick out your finger, and spin around three times. When you open your eyes, you are pointing directly at Peter's sister, Paula Pivot. You say, "Quickly! Those of you who are still standing. If you're shorter than Paula, come stand over here. If you're taller than Paula, go stand over there. If you're the same height, you can go into either group."

The children shuffle around, and soon they are standing in the two groups. You count and find 59 children in the shorter group, and 60 children in the taller group. You know the 98th shortest child must be in the taller group, so you tell Paula and the 59 shorter children to sit in the bleachers.

You again close your eyes, stick out your finger, and spin around three times. When you open your eyes, you are pointing directly at Paula's cousin, Prudence Pivot. You say, "Quickly! Those of you who are still standing. If you're shorter than Prudence, come stand over here. If you're taller than Prudence, go stand over there. If you're the same height, you can go into either group."

The children shuffle around, and soon they are standing in the two groups. You count and find 37 children in the shorter group, and 22 children in the taller group. You know that Paula and 59 other shorter children are sitting on the bleachers. Along with the 37 shorter children still standing, you know that a total of 97 children are shorter than Prudence. Therefore, Prudence is the 98th shortest child!

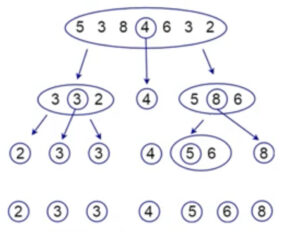
Сортировка рекурсивным слиянием (merge sort; recursive sorting algorithm) с двоичным делением

Основной принцип работы:

1) принцип подготовки к сортировке: объединяем два заведомо отсортированных списка (в том числе из одного элемента – выход из рекурсии) в отсортированный список

2) принцип самой сортировки:

• • при сравнении значений в списках перемещаем индекс того массива, значение в котором меньшее
  • мы знаем, что каждый из двух массивов отсортирован на входе в функцию заведомо, это позволяет после того, как мы элемент исходного списка поместили в результирующий этот элемен отбросить из анализа и перейти к следующему, не возвращаясь к этому элементу еще раз для смещения в рамках результирующего списка т.е. case “пришел элемент менее того, который уже в результирующем массиве” заведомо невозможен

Скорость алгоритма около 2 секунд (Core i5 2133 MHHz) на 100 тыс. рандомизированных чисел от -100 тыс до 100 тыс.

 def merge_sort(to_sort1: list, to_sort2: list) -> list:
    '''Реализует сортировку & объединение двух заведомо 
    отсортированных массивов'''
    result_arr = []
    i1 = 0
    i2 = 0
    while i1 <= len(to_sort1)-1 and i2 <= len(to_sort2)-1:
        if to_sort1[i1] < to_sort2[i2]:
            result_arr.append(to_sort1[i1])
            i1+=1
        else:
            result_arr.append(to_sort2[i2])
            i2+=1
    for value in to_sort1[i1:]:
        result_arr.append(value)
    for value in to_sort2[i2:]:
        result_arr.append(value)
    return result_arr

def split_and_merge_sort_recursive(to_sort: list) -> list:
    '''Реализует split двух массивов до минимального ([] или [n])
    с последующим рекурсивным вызовом merge_sort'''
    if len(to_sort) < 2:
        return to_sort
    middle = len(to_sort) // 2
    to_sort1 = to_sort[:middle]
    to_sort2 = to_sort[middle:]
    return merge_sort(split_and_merge_sort_recursive(to_sort1),
                    split_and_merge_sort_recursive(to_sort2))

array = [677, 234, 15, 222222, 3, 9, 2, 3, 6, 12, 234, 11, 1, -100, -234, -55, 123124, 444]
print(split_and_merge_sort_recursive(array))

>>>
[-234, -100, -55, 1, 2, 3, 3, 6, 9, 11, 12, 15, 234, 234, 444, 677, 123124, 222222

Простые задачи stepik

Хорошая задача, показывающая как важна визуализация тестовых данных и написание краевых случаев. На числовой прямой даны два отрезка: [a1;b1] и [a2;b2]. Напишите программу, которая находит их пересечение. Пересечением двух отрезков может быть: отрезок; точка; пустое множество.  На вход программе подаются 4 целых числа a1,b1,a2,b2, каждое на отдельной строке. Гарантируется, что a1<b1​ и a2<b2​.

a = int(input())
b = int(input())
c = int(input())
d = int(input())

intersect1 = max(a,c)
intersect2 = min(d,b)
if intersect2 < intersect1:
    print("пустое множество")
elif intersect1 == intersect2:
    print(intersect1)
else:
    print(max(a,c), min(d,b))

Проверка на то, что треугольник существует (выполняется неравенство треугольника). Площадь треугольника, кстати, находится по формулам (любая):

• • (A*H)/2 – произведение основания на высоту/2
  • (B*C)/2 – произведение катетов/2

a=int(input())
b=int(input())
c=int(input())
if a < (b+c) and b < (a+c) and c < (a+b):
    print("YES")
else:
    print("NO")

Заданы две клетки шахматной доски. Напишите программу, которая определяет имеют ли указанные клетки один цвет или нет. Если они покрашены в один цвет, то выведите слово «YES», а если в разные цвета — то «NO».

if (a + b) % 2 == (c + d) % 2:  # белые на четных, черные на нечетных
  print("YES")

Даны две различные клетки шахматной доски. Напишите программу, которая определяет, может ли слон попасть с первой клетки на вторую одним ходом. Программа получает на вход четыре числа от 1 до 8 каждое, задающие номер столбца и номер строки сначала для первой клетки, потом для второй клетки. Программа должна вывести «YES», если из первой клетки ходом слона можно попасть во вторую или «NO» в противном случае. Вместо abs() можно было использовать возведение в степень ^2 т.к. отрицательное число в четной степени положительно (в нечетной сохраняет отрицательный знак).

if abs(a-c) == abs(d-b):  
# разность точек БЫЛО-СТАЛО всегда одинакова для слона, целочисленное деление/возведение в степень/вычитание из старшего элемента младшего, для исключения из условия знака
# ферзь аналогично слону + диагональ может быть одна и та же
  print("YES")

Даны две различные клетки шахматной доски. Напишите программу, которая определяет, может ли конь попасть с первой клетки на вторую одним ходом. Программа получает на вход четыре числа от 1 до 8 каждое, задающие номер столбца и номер строки сначала для первой клетки, потом для второй клетки. Программа должна вывести «YES», если из первой клетки ходом коня можно попасть во вторую или «NO» в противном случае.

if (abs(a-c) == 2 and abs(b-d) == 1) or (abs(a-c) == 1 and abs(b-d) == 2):  # всегда передвижение на одну клетку в одну сторону и две клетки в другую, по аналогии со слоном отбрасываем знак
  print("YES")

Программа должна вывести «YES», если из первой клетки ходом короля можно попасть во вторую, или «NO» в противном случае. На вход программе подаётся четыре числа от 1 до 8.

a=int(input())
b=int(input())
c=int(input())
d=int(input())
if (a==c or (a+1)==c or (a-1)==c) and (b==d or (b+1)==d or (b-1)==d):
    print("YES")
else:
    print("NO")

Напишите программу, которая определяет, являются ли три заданных числа (в указанном порядке) последовательными членами арифметической прогрессии.

a = int(input())
b = int(input())
c = int(input())
if (c-b) == (b-a):
    print("YES")
else:
    print("NO")

Напишите программу, которая определяет наименьшее из четырёх чисел. ((без использования MIN на без “чистых if”))

a = int(input())
b = int(input())
c = int(input())
d = int(input())
minn = a
if minn > b:
    minn = b
if minn > c:
    minn = c
if minn > d:
    minn = d
print(minn)

Напишите программу, которая считывает три числа и подсчитывает сумму только положительных чисел.

a = int(input())
b = int(input())
c = int(input())
summ = 0
if a > 0:
    summ = summ + a
if b > 0:
    summ = summ + b
if c > 0:
    summ = summ + c
print(summ)

Найти первую цифра после точки во float числе (без split/index).

a=float(input())
print(int((a*10)%10))

Найти только дробную часть числа float.

a=float(input())
b=int(a)
print(a-b)  # var1
print(a%1)  # var2

Сортировка трех чисел без использования сортировки.

dmax = max(a,b,c)
dmin = min(a,b,c)
davr = a+b+c-dmax-dmin